| Sintesi per tentativi del controllo | Controllo di un impianto a levitazione magnetica | Esercitazione 6 |
Data la seguente funzione di trasferimento ad anello aperto:
10
G(s)=-------------------
s(s/10 + 1)
Si vuole che il sistema retroazionato con retroazione unitaria e con l'aggiunta di un opportuno compensatore in serie soddisfi le seguenti specifiche:
Abbia costante di velocità Kv=100;
Abbia un margine di fase mf>50°
Abbia un errore di riproduzione dei segnali sinusoidali con pulsazione w<1 rad/sec che sia <10%
Abbia un'attenuazione dei segnali sinusoidali con pulsazione w>100 rad/sec che sia >95%(le ultime due specifiche si traducono in una richiesta di banda passante in catena chiusa wb=10rad/sec, in seguito è riportata la spiegazione di questa affermazione)
E' possibile utilizzare direttamente l'M-file disponibile in progettocontrollo.m
%file per il
progetto del controllo del
%controllo di un generico impianto
%funzioni di trasferimento dell'impianto
num=10
den=[1/10 1 0]
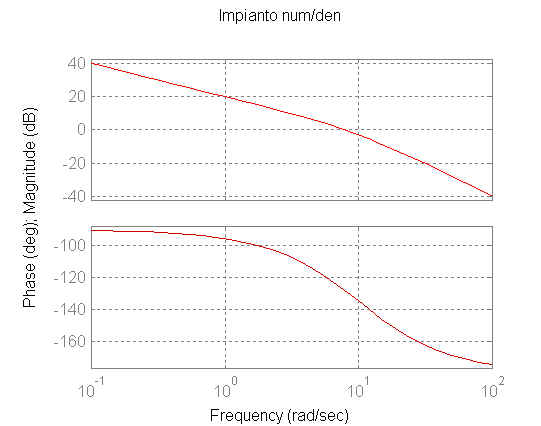
figure(1)
bode(num,den)
title('Impianto
num/den')
grid

Per soddisfare la specifica sul guadagno di velocità o errore di inseguimento alla rampa, è necessario avere un guadagno di velocità, dovuto alla serie dei blocchi di controllo e di impianto pari a 100, visto che il guadagno di velocità dell'impianto vale 10, si rende necessaria l'aggiunta di un ulteriore guadagno.
%metto a posto il guadagno di anello, kp kv ka
num1=num*10;
den1=den;
Potrebbe essere necessario, a questo punto inserire un integratore, se le specifiche lo richiedono, in questo caso abbiamo già un polo nell'origine dovuto all'impianto, per cui non è necessario inserire un ulteriore polo. La posizione dello zero deve essere scelta in modo da non andare oltre la banda del sistema in catena chiusa.
%inserisco l'eventuale integratore
%num1=conv(num1,[1/0.1
1];
%den1=conv(den1,[1/0.1 0]);
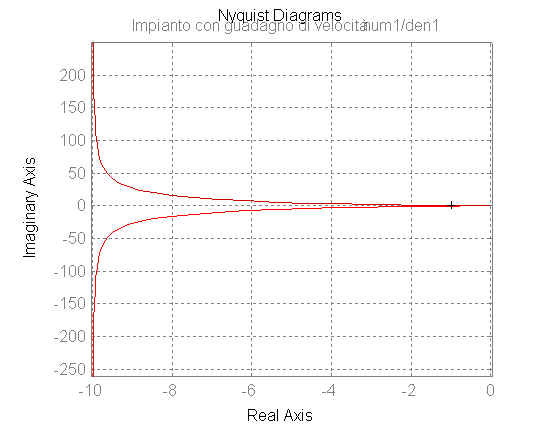
Dopo aver inserito nel compensatore tutte le parti necessarie per il rispetto delle prime specifiche, bisogna verificare sul diagramma di Nyquist, come può essere ottenuta la stabilità del sistema. Potrebbe essere necessario scegliere un opportuno segno del guadagno stazionario del compensatore.
%verifica della stabilità tramite il diagramma di Nyquist
figure(2)
nyquist(num1,den1);
title('Impianto
con guadagno di velocità num1/den1')
zoom on
grid
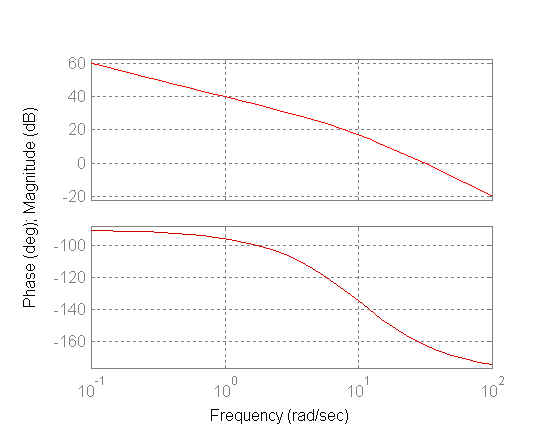
figure(3)
bode(num1,den1);
title('Impianto
con guadagno di velocità num1/den1')
zoom on
grid
Se fosse necessario cambiare il segno del compensatore, bisogna farlo prima di partire con il progetto della rete anticipatrice o attenuatrice.
%scelta del
segno della retroazione
%num1=-num1;
%den1=den1;
Scelgo una banda pari a 10 rad/sec per soddisfare la specifica relativa ai segnali sinusoidali con pulsazione w=1 rad/sec progetto la rete anticipatrice in wt=0.7*10=7 e wt=1 con coefficiente ma=1.5, recuperando circa 20°
%progetto della rete anticipatrice
wt=7;
omegatau=1;
tau=omegatau/wt;
ma=1.5;
numc=[tau 1];
denc=[tau/ma 1];
Nel caso sia necessario recuperare altra fase, si progetta un'ulteriore rete anticipatrice con gli stessi passi utilizzati in precedenza.
figure(4)
bode(numc,denc)
title('Rete
anticipatrice numc/denc')
grid
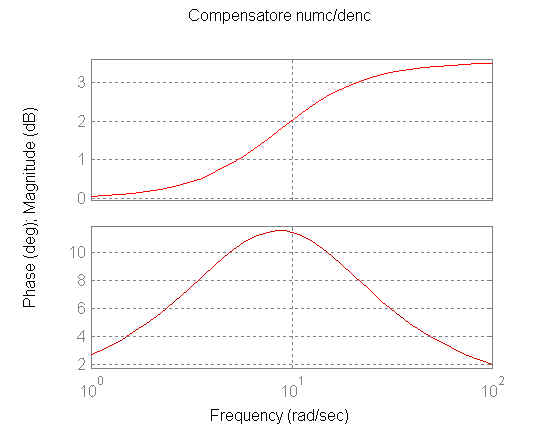
Una volta progettata la rete anticipatrice è necessario verificare il nuovo diagramma di Bode in catena aperta, per capire quanto deve essere, eventualmente, attenuato il modulo in prossimità della frequenza di cross-over wt
[numca,denca]=series(numc,denc,num1,den1);
figure(5)
bode(numca,denca)
title('Impianto
in catena aperta numca/denca')
grid
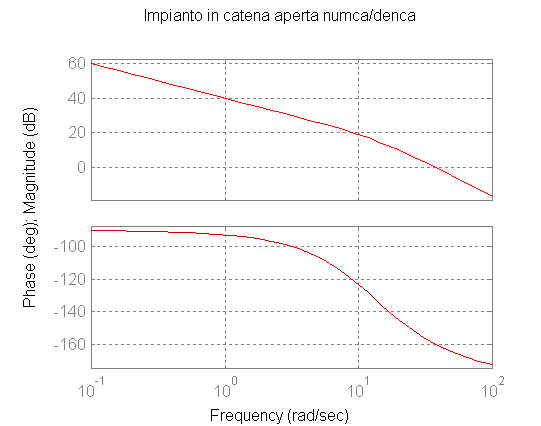
Devo attenuare il modulo alla frequenza wc in modo da avere l'attraversamento dello 0dB. Inoltre per le frequenze superiori a 0.7 rad/sec devo attenuare il modulo in modo da soddisfare la quarta specifica.
Calcolo il valore esatto del modulo alla frequenza wt
wt=7;
[mag,pha]=bode(numca,denca,wt);
Conosciuto il valore di cui devo attenuare vado a cercare sugli abachi il coefficiente mi tale da portare a quel valore di attenuazione in wt=100
%progetto la rete attenuatrice
wt=7;
tau=100/wt;
mi=mag;
numci=[tau/mi 1];
denci=[tau 1];
figure(6)
bode(numci,denci);
title('Rete
attenuatrice numci/denci')
grid
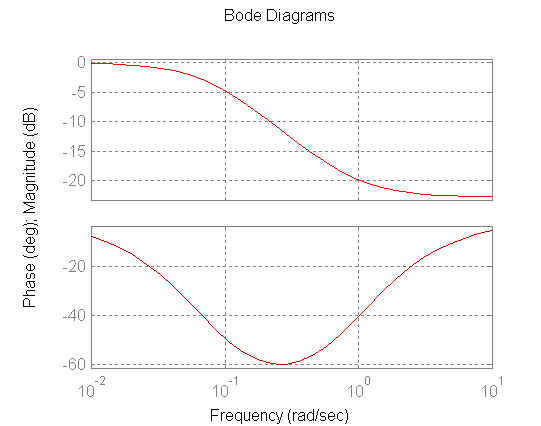
Vado ora a verificare se il nuovo diagramma di Bode risponde alle specifiche di modulo e fase richiesti
[numca1,denca1]=series(numca,denca,numci,denci);
figure(7)
bode(numca1,denca1)
%margin(numcc,dencc)
title('Impianto
in catena aperta numca1/denca1')
zoom on
grid
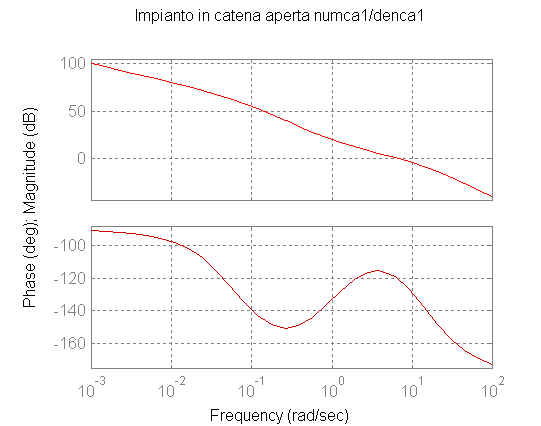
Dal momento che le specifiche rispondono alle richieste è ora possibile chiudere l'anello di retroazione.
%chiusura dell'anello e verifica delle specifiche
[numcc,dencc]=cloop(numca1,denca1);
figure(8)
bode(numcc,dencc)
title('Impianto
in catena chiusa numcc/dencc')
grid
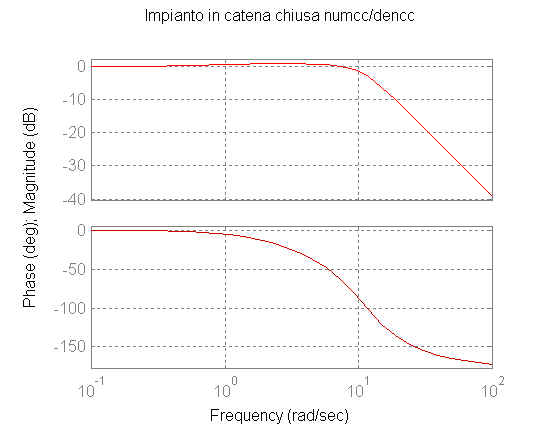
figure(9)
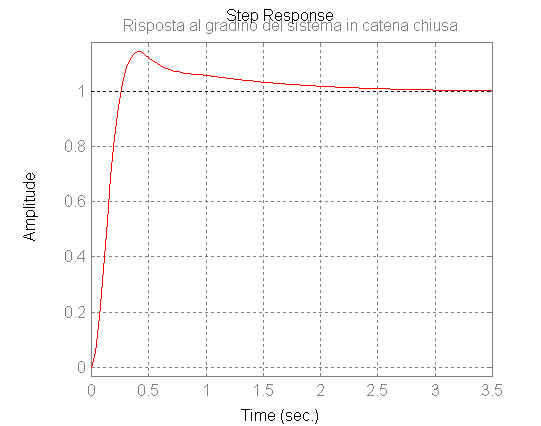
step(numcc,dencc)
title('Risposta
al gradino del sistema in catena chiusa')
grid
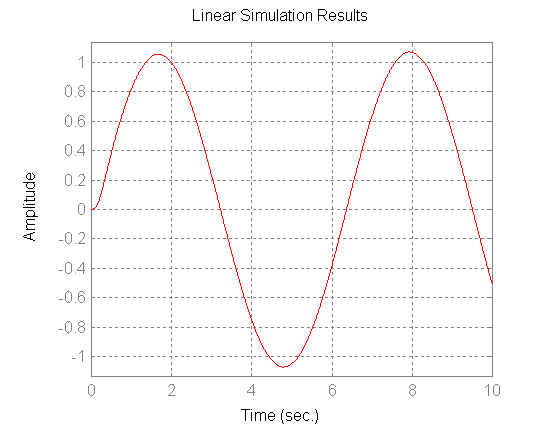
w=1;
t=0:0.01:10;
y=sin(w*t);
figure(10)
lsim(numcc,dencc,y,t)
grid
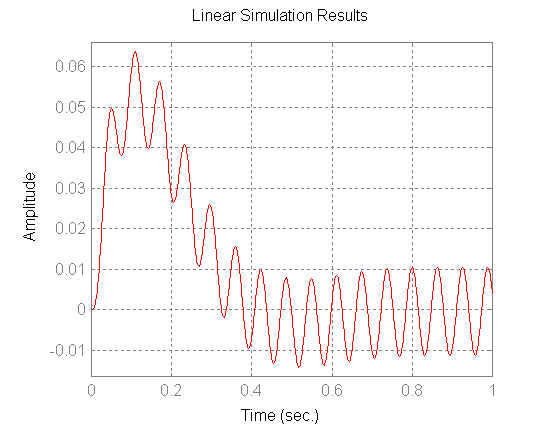
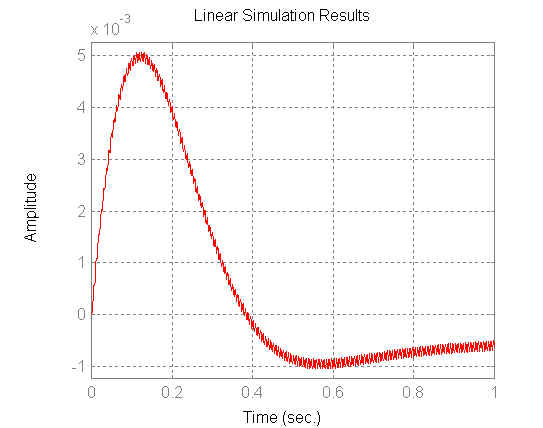
w=100;
t=0:0.001:1;
y=sin(w*t);
figure(11)
lsim(numcc,dencc,y,t)
grid
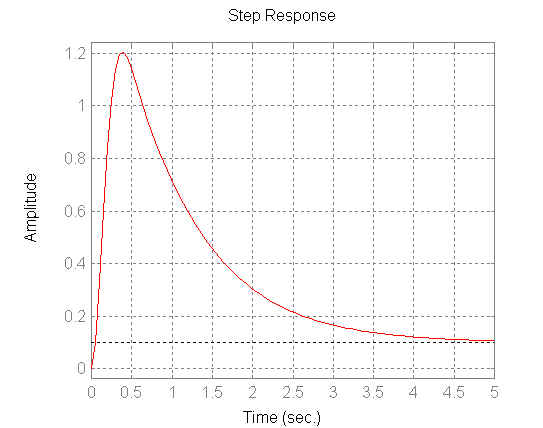
Tra le verifiche potrebbe essere necessario inserire anche la verifica della specifica sull'attività sul comando, a questo scopo si possono utilizzare le seguenti righe di comando:
[numcompensatore,dencompensatore]=series(kc*numc,denc,numci,denci);
[numcomando,dencomando]=feedback(num,den,numcompensatore,dencompensatore);figure(12)
step(numcomando,dencomando);
title('attività
sul comando con ingresso a gradino');
grid
%ingresso sinusoidale ad alta frequenza
w=1000;
t=0:0.001:1;
y=sin(w*t);
figure(13)
lsim(numcomando,dencomando,y,t)
title('attività
sul comando con ingresso sinusoidale')
grid
Il compensatore assume la seguente forma:
